18.01 Exercises

Problem Set 1

Unit 1: Differentiation

1A Graphing: 1b, 2b, 3a, 3b, 3e, 6b, 7b

1B Velocity and rates of change: 1a, 1b, 1c

1C Slope and derivative: 1a, 3a, 3b, 3e, 4a, 4b, 5, 6, 2

1D Limits and continuity: 1a, 1c, 1d, 1f, 1g, 3a, 3c, 3d, 3e, 6a, 8a

1E Differentiation formulas, polynomials, products, quotients: 1a, 1c, 2b, 3, 4b, 5a, 5c

1F Chain rule, implicit differentiation: 1a, 1b, 2, 6, 7b, 7c

1J Trigonometric functions, continues: 1a, 1k, 1m

1G Higher derivatives: 1b, 1c, 5a

Answers as follows:

1A Graphing

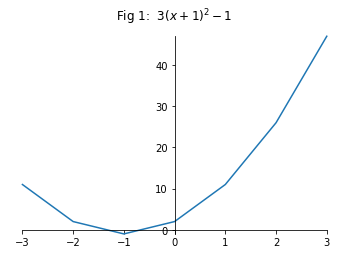
1A-1: By completing the square, use translation and change of scale to sketch:

b) $y = 3x^2 + 6x + 2$

To complete the square we need to do some algebraic work considering the form of the equation $a^2 + b + c$, we take $\left( \frac {b} {2} \right)^2$ to create the square $(a + \left( \frac {b} {2} \right))^2 - \left( \frac {b} {2} \right)^2 + c$

$\left( \frac {b} {2} \right)$ = 3 and $\left( \frac {b} {2} \right)^2 = 9$

Therefore our completed square equation is $3(x+1)^2 -1$

#import necessary modules to sketch the graph
import math
import numpy as np
import matplotlib.pyplot as plt

x = range(-3,4,1)
y = []

for xi in x:
    equation = 3*(xi + 1)**2 - 1
    y.append(equation)

fig, ax = plt.subplots()

ax.plot(x,y)

ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_title('Fig 1:  $3(x + 1)^2 -1$')

Text(0.5, 1.0, 'Fig 1:  $3(x + 1)^2 -1$')

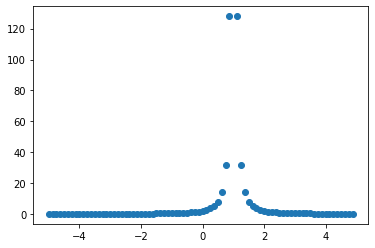
1A-2: Sketch, using translation and change of scale:

b) $y = \frac {2} {(x - 1)^2}$

'''
Note in this exercise there is a zero division issue so our range
is set to skip the issue by exluding 1
'''
y = []
a = []
for i in [x for x in np.arange(-5,5, .125) if x != 1]:
        a.append(i)
        equation = 2 / (i - 1)**2
        y.append(equation)

plt.scatter(a, y)

<matplotlib.collections.PathCollection at 0x1e606030248>

1A-3: Identify each of the following as even, odd, or neither

a) $\frac {x^3 + 3x} {1 - x^4}$

'''
I went ahead and graphed this although not necessary
'''
y = []
a = []
for i in [x for x in np.arange(-2.0,2.5, .125) if x != 1 and x != -1]:
        a.append(i)
        equation = (i**3 + 3 * i)/(1 - i**4)
        y.append(equation)

plt.scatter(a,y)

<matplotlib.collections.PathCollection at 0x1e6060e7d88>

'''
The function eq takes 1 parameter so that we can test for even, odd, or neither.
Using logic we use multiple print statements to print the correct answer.
'''
def eq(x):
    return (x**3 + 3 * x)/(1 - x**4)

a = eq(-2)
b = -eq(2)

even = a == b #If true then even

odd = a + b == 0 #If true then odd

neither = even == False and odd == False #If true then neither

if even == True:
    print('The function is even')
elif odd == True:
    print('The function is odd')
elif neither == True:
    print('The function is neither even or odd')
else:
    print('Ooops, better check your math again')

The function is even

a) $\sin^2x$

x = np.arange(-1, 1.1, .1)
y = []

for xi in x:

    eq = math.sin(xi)**2
    y.append(eq)

plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x1e606176f48>]

def eq(x):
    return math.sin(x)**2

a = eq(-2)
b = -eq(2)

even = a == b #If true then odd

odd = a + b == 0 #If true then even

neither = even == False and odd == False #If true then neither

if even == True:
    print('The function is even')
elif odd == True:
    print('The function is odd')
elif neither == True:
    print('The function is neither even or odd')
else:
    print('Ooops, better check your math again')

The function is odd

c) $\frac {\tan{x}} {1 + x^2}$

This isn’t a required problem but used for a neither result

def eq(x):
    return (1-x)**4

a = eq(-2)
b = -eq(2)

even = a == b #If true then odd

odd = a + b == 0 #If true then even

neither = even == False and odd == False #If true then neither

if even == True:
    print('The function is even')
elif odd == True:
    print('The function is odd')
elif neither == True:
    print('The function is neither even or odd')
else:
    print('Ooops, better check your math again')

The function is neither even or odd

1A-6: Express in the form Asin(x+c)

b) $\sin{x} - \cos{x}$

1A-7: Find the period, amplitude, and phase angle, and use these to sketch

b) $-4\cos(x + \frac {\pi} {2})$

1B Velocity and rates of change

1B-1: A test tube is knocked off a tower at the top of the Green building. For the purposes of this experiment the tower is 400 feet above the ground, and all the air in the vicinity of the Green building was evacuated, so as to eliminate wind resistance. The test tube drops $16ft^2$ in $t$ seconds. Calculate:

a) the average speed in the first two seconds of the fall,

k = 16*2**2

k = 16*2**2
o = ((400 - k) - 400)/2

print('The average speed in the first two seconds of falling was', o)

The average speed in the first two seconds of falling was -32.0

b) the average speed in the last two seconds of the fall,

l = 16*3**2
m = 16*5**2
o = ((400-m) - (400 - l))/2

print('The average speed in the last two seconds of falling was', o)

The average speed in the last two seconds of falling was -128.0

c) and the instantaneous speed at landing.

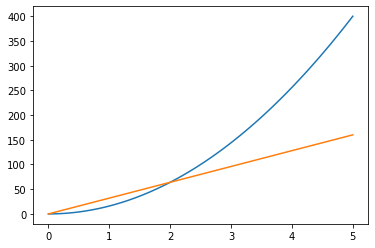
def derivative(f, a, h=.001):
    return(f(a + h) - f(a - h)) / (2 * h)

t = np.linspace(0, 5, 100)
f = lambda t: 16*t**2
y = f(t)
dydx = derivative(f,t)

plt.plot(t,y)
plt.plot(t,dydx)

terminal_speed = derivative(f, 5)
print('The instantaneous speed at landing was', round(terminal_speed, 2))

The instantaneous speed at landing was 160.0

1C: Slope and Derivative

1C-1: Use the difference quotient definition of derivative to calculate the rate of change of the area of a disk with respect to its radius.

a) $\frac {f(x + h) - f(x)} {h}$

Circumference formula is $\pi r^2$ so we get $\frac {\pi(r + h)^2 - \pi r^2} {h}$

1C-3: Calculate the derivative of each of these functions directly from the definition:

a) $f(x) = \frac {1} {(2x + 1)}$

$$ f’(x) = \frac {1} {h} \left(\frac {1} {2(x+h)+1} - \frac{1}{2x+1}\right)$$

The calculus part is down and it’s now time to simplify this problem as best possible so that we can attempt to find a result as $h$ approaches 0. The problem reduces to the following:

$$ f’(x) = \frac {-2} {(2(x+h)+1)(2x+1)} \to \lim_{h \to 0} \frac{-2}{(2x+1)^2}$$

b) $f(x)=2x^2 +5x +4$

$$ f’(x) = \frac {1} {h} \left(2(x+h)^2+ 5(x+h)+4 - (2x^2+5x+4)\right)$$

$$ f’(x) = 4x + 2h + 5 \to \lim_{h \to 0}\left(4x + 5\right)$$

e) For 3a and 3b find the points where the slope is $+1$, $-1$, and $0$.

Examining 3a we know $\frac{-2} {(2x + 1)^2} < 0$ so there are no solutions for $+1$ or $0$.

For $-1$ we find: $\frac{-2} {(2x + 1)^2} = -1 \Rightarrow x = \frac {\pm\sqrt{2} - 1} {2}$

Examining 3b we get the following:

$$4x + 5 = 1 \Rightarrow x = -1$$

$$4x + 5 = 0 \Rightarrow x = \frac {-5} {4}$$

$$4x + 5 = -1 \Rightarrow x = \frac {-3} {2}$$

1C-4: Write an equation for the tangent line for the following functions

a)

b)

1C-5: Find all tangent lines through the origin to the graph of $y = 1+(x-1)^2$

1C-6: Graph the derivative of the following functions directly below the graph of the function. It is very helpful to know that the derivative of an odd function is even and the derivative of an even function is odd(see 1F-6).

1C-2: Let $f(x) = (x-a)g(x)$. Use the definition of the derivative to calculate that $f’(a) = g(a)$, assuming that $g$ is continuous.

1D: Limits and continuity

1D-1: Calculate the following limits if they exist. If they do not exist, then indicate whether they are $+\infty$ or $-\infty$ or undefined.

a) $\lim_{x \to 0}\left(\frac{4}{x-1}\right)$

c) $\lim_{x \to -2}\left(\frac{4^2}{x+2}\right)$